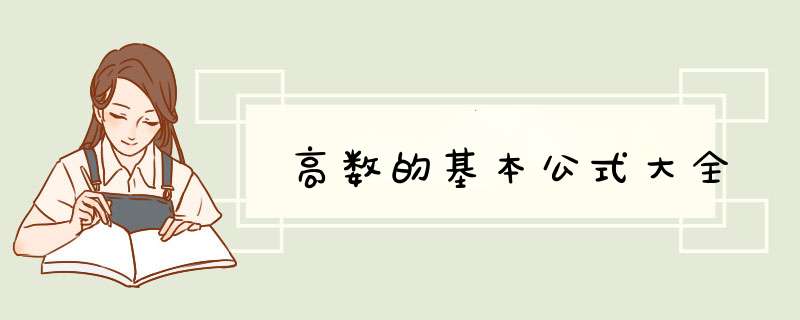
高数的基本公式大全

高数的基本公式大全如下：

1、数学公式：抛物线标准方程 y^2=2px y^2=-2px x^2=2py x^2=-2py。直棱柱侧面积 S=ch。斜棱柱侧面积 S=ch。正棱锥侧面积 S=1/2ch。正棱台侧面积 S=1/2(c+c)h。圆台侧面积 S=1/2(c+c)l=pi(R+r)l。球的表面积 S=4pir2。

2、圆柱侧面积 S=ch=2πh。圆锥侧面积 S=1/2cl=πrl。弧长公式 l=ar a是圆心角的弧度数r >0。扇形面积公式 s=1/2lr。锥体体积公式 V=1/3SH。

圆锥体体积公式 V=1/3pir2h。斜棱柱体积 V=SL 注：其中，S是直截面面积， L是侧棱长，柱体体积公式 V=sh。

对数函数基本性质：

1、过定点(1,0)，即x=1时，y=0。

2、当 0<a<1 时，在(0，+∞)上是减函数;当a>1时，在(0，+∞)上是增函数。

3、对数函数是非奇非偶函数（无论增函数还是减函数都一样），它的反函数指数函数同样也是非奇非偶函数。

高数公式：

1、导数公式

2、基本积分表

公式

3、三角函数的有理式积分

4、初等函数

5、两个重要极限

6、三角函数公式

7、和差角公式

8、和差化积公式

9、倍角公式

10、半角公式

11、正玄余弦公式

12、莱布尼兹公式、中值定理、曲率

13、定积分应用相关公式

14、空间几何

15、平面方程

16、二次曲面

17、多元函数微分

18、多元复合函数及应用

19、隐函数求导

20、微分在几何上的应用

21、方向导数与梯度

22、多元函数极值

23、重积分及应用

24、柱面坐标和球面坐标

25、曲线积分

26、曲面积分

高数需求函数的公式：q=a-bp。

需求价格弹性=需求变动百分比/收入变动百分比。 即Ed=(△Q/Q)/(△Y/Y）需求的价格弧弹性的中点公式：Ed=-△Q/△P●(（P1+P2）/2)/((Q1+Q2)/2)，主要决定因素：商品的价格、消费者收入水平、相关商品的价格、消费者的偏好和消费者对该商品的价格预期等。

常见的需求函数有以下几种形式：

D=（a-P）/b（a，b大于0）。

D=（a-P平方）/b（a，b大于0）。

 D=（a-√p）/b（a，b大于0）。

其中P表示商品价格。

高数三角函数公式如下：

1、公式一，设a为任意角，终边相同的角的同一三角函数的值相等：

2、公式二，设a为任意角，Π+a与a的三角函数值之间的关系：

3、公式三，任意角-a与a的三角函数值之间的关系：

4、公式四，Π-a与a的三角函数值之间的关系：

5、公式五，2Π-a与a的三角函数值之间的关系：

记背诀窍：奇变偶不变，符号看象限。奇变偶不变是指其中的奇偶是指π/2的奇偶数倍，变与不变是指三角函数名称的变化，若变，则是正弦变余弦，正切变余切。符号看象限是指根据角的范围以及三角函数在哪个象限的正负，来判断新三角函数的符号。

三角函数是数学中属于初等函数中的超越函数的函数。它们的本质是任何角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的。其定义域为整个实数域。另一种定义是在直角三角形中，但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解，将其定义扩展到复数系。

高数常见函数求导公式如下图：

求导是数学计算中的一个计算方法，它的定义就是，当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。

在一个函数存在导数时，称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。

扩展资料：

一阶导数表示的是函数的变化率，最直观的表现就在于函数的单调性，定理：设f(x)在[a,b]上连续，在（a,b)内具有一阶导数，那么：

（1）若在(a,b)内f'(x)>0,则f(x)在[a,b]上的图形单调递增；

（2）若在(a,b)内f’(x)<0,则f(x)在[a,b]上的图形单调递减；

（3）若在(a,b)内f'(x)=0,则f(x)在[a,b]上的图形是平行（或重合）于x轴的直线，即在[a,b]上为常数。

函数的导数就是一点上的切线的斜率。当函数单调递增时，斜率为正，函数单调递减时，斜率为负。

导数与微分：微分也是一种线性描述函数在一点附近变化的方式。微分和导数是两个不同的概念。但是，对一元函数来说，可微与可导是完全等价的。

可微的函数，其微分等于导数乘以自变量的微分dx，换句话说，函数的微分与自变量的微分之商等于该函数的导数。因此，导数也叫做微商。函数y=f(x)的微分又可记作dy=f'(x)dx。