数列 0+1+3+6+10…… 求和公式是什么？

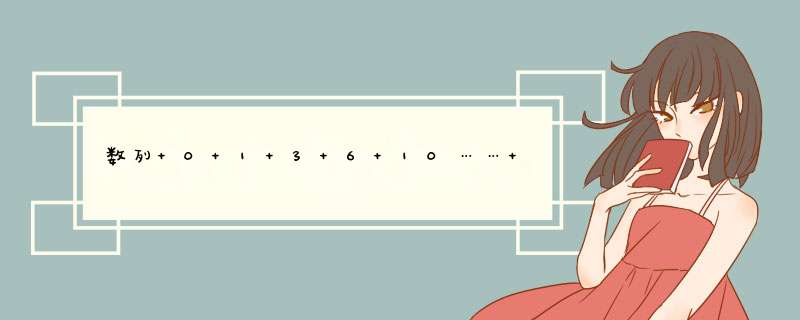
数列的排列规律为：

a1=0；a2=0+1=1；a3=0+1+2=3；a4=0+1+2+3=6；……

有等差数列求和公式可知

an=(n-1)n/2=½(n²-n)

Sn=½[(1²-1)+(2²-2)+(3²-3)+……+(n²-n)]

=½[(1²+2²+3²+……+n²)-(1+2+3+……+n)]

=½[n(n+1)(2n+1)/6-(n+1)n/2]

=(n³-n)/6

数列0+1+3+6+10……

求和公式为：(n³-n)/6

注：如1²+2²+3²+……+n²=n(n+1)(2n+1)/6不解，请追问。

斐波那契数列求和公式如下：

斐波那契数列前n项和公式是F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N）。

这个数列从第3项开始，每一项都等于前两项之和。

斐波那契数列的定义者，是意大利数学家莱昂纳多·斐波那契（Leonardo Fibonacci），生于公元1170年，卒于1250年，籍贯是比萨。他被人称作“比萨的莱昂纳多”。1202年，他撰写了《算盘全书》（Liber Abacci）一书。

他是第一个研究了印度和阿拉伯数学理论的欧洲人。他的父亲被比萨的一家商业团体聘任为外交领事，派驻地点于阿尔及利亚地区，莱昂纳多因此得以在一个阿拉伯老师的指导下研究数学。他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯等地研究数学。另外斐波纳契还在计算机C语言程序题中应用广泛。

斐波那契数列的平方与前后项：

从第二项开始（构成一个新数列，第一项为1，第二项为2，……），每个偶数项的平方都比前后两项之积多1，每个奇数项的平方都比前后两项之积少1。

如：第二项 1 的平方比它的前一项 1 和它的后一项 2 的积 2 少 1，第三项 2 的平方比它的前一项 1 和它的后一项 3 的积 3 多 1。

注：奇数项和偶数项是指项数的奇偶，而并不是指数列的数字本身的奇偶，比如从数列第二项 1 开始数，第 4 项 5 是奇数，但它是偶数项，如果认为 5 是奇数项，那就误解题意，怎么都说不通。

　数列求和的七种 方法 ：倒序相加法、分组求和法、错位相减法、裂项相消法、乘公比错项相减(等差×等比)、公式法、迭加法。下面是我给大家带来的数列求和的七种方法，希望能够帮助到大家!

　高中数学数列求和的七种方法

　1、倒序相加法

　倒序相加法如果一个数列{an}满足与首末两项等“距离”的两项的和相等(或等于同一常数)，那么求这个数列的前n项和，可用倒序相加法。

　2、分组求和法

　分组求和法一个数列的通项公式是由几个等差或等比或可求和的数列的通项公式组成，求和时可用分组求和法，分别求和而后相加。

　3、错位相减法

　错位相减法如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么这个数列的前n项和可用此法来求，如等比数列的前n项和公式就是用此法推导的。

　4、裂项相消法

　裂项相消法把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得其和。

　5、乘公比错项相减(等差×等比)

　这种方法是在推导等比数列的前n项和公式时所用的方法，这种方法主要用于求数列{an×bn}的前n项和，其中{an}，{bn}分别是等差数列和等比数列。

　6、公式法

　对等差数列、等比数列，求前n项和Sn可直接用等差、等比数列的前n项和公式进行求解。运用公式求解的注意事项：首先要注意公式的应用范围，确定公式适用于这个数列之后，再计算。

　7、迭加法

　主要应用于数列{an}满足an+1=an+f(n)，其中f(n)是等差数列或等比数列的条件下，可把这个式子变成an+1-an=f(n)，代入各项，得到一系列式子，把所有的式子加到一起，经过整理，可求出an，从而求出Sn。

相关 文章 ：

1 高中数学无穷递降等比数列求和公式

2 高中数学学习方法和技巧是什么

3 高中数学常考题型答题技巧与方法及顺口溜

4 2019年秋季高中数学新教材变化之处和12个答题模板

5 高一数学的学习方法及特点

1公式法：

等差数列求和公式:

Sn=n(a1+an)/2=na1+n(n-1)d/2

等比数列求和公式：

Sn=na1(q=1) Sn=a1(1-q^n)/(1-q)=(a1-an×q)/(1-q) (q≠1)

其他

1+2^2+3^2+4^2++n^2=n(n+1)(2n+1)/6

1+2^3+3^3+4^3++n^3=[n(n+1)/2]^2

2错位相减法

适用题型：适用于通项公式为等差的一次函数乘以等比的数列形式 和等差等比数列相乘 { an }、{ bn }分别是等差数列和等比数列Sn=a1b1+a2b2+a3b3++anbn

例如：

an=a1+(n-1)d

bn=b1·q^(n-1)

Cn=anbn

Tn=a1b1+a2b2+a3b3+a4b4+anbn

qTn= a1b2+a2b3+a3b4++a(n-1)bn+anb(n+1)

Tn-qTn= a1b1+b2(a2-a1)+b3(a3-a2)+bn[an-a(n-1)]-anb(n+1)

Tn(1-q)=a1b1-anb(n+1)+d(b2+b3+b4+bn) ______①

=a1b1-an·b1·q^n+d·b2[1-q^(n-1)]/(1-q)

=a1b1-(a1+nd-d)·b1q^n+d·b2[1-q^(n-1)]/(1-q)

Tn=上述式子/(1-q)

此外①式可变形为

Tn(1-q)=a1b1-anb(n+1)+d(Sn-b1) Sn为{bn}的前n项和

此形式更理解也好记

3倒序相加法

这是推导等差数列的前n项和公式时所用的方法,就是将一个数列倒过来排列（反序）,再把它与原数列相加,就可以得到n个(a1+an)

Sn =a1+ a2+ a3++an

Sn =an+ a(n-1)+a(n-2)+a1

上下相加 得到2Sn 即 Sn= （a1+an)n/2

4分组法

有一类数列,既不是等差数列,也不是等比数列,若将这类数列适当拆开,可分为几个等差、等比或常见的数列,然后分别求和,再将其合并即可

例如：an=2^n+n-1

5裂项法

适用于分式形式的通项公式,把一项拆成两个或多个的差的形式,即an=f(n+1)－f(n),然后累加时抵消中间的许多项

常用公式：

（1）1/n(n+1)=1/n-1/(n+1) ,1/（n-1）-1/n

等比数列求和公式为Sn=a1(1-q^n)/(1-q)。

1、等比数列常用公式。

等比数列是指一个数列中每个数与它的前一个数的比例都相等的数列。其公式为：an=a1× r^(n-1)。其中，an是数列的第n项，a1是数列的第1项，r是固定的比例系数，n是项数。而等比数列的前n项和公式为：Sn=a1×(1-r^n)/(1-r)。

其中，Sn表示数列的前n项和，a1是数列的第1项，r是固定的比例系数，n是项数。这个公式的中分子是根据等比数列的求和公式推导的，等比数列的前n项和公式为：Sn=a1×(1-r^n)/ (1-r)。

简单解释一下，分子就是数列前n项相加的结果，分母是一个定值，用来保证分子与后面项的和的比例都一样。这个公式可以方便地计算等比数列的前n项和，也是数学中常用的公式之一。

2、需要注意的事项。

在应用等比数列的公式计算时，要先使用$a_1$和$q$确定数列的特征，然后根据需要求取特定项或前n项的和。此外，还需要注意选择适当的计算方式，并注意公式中各参数的含义。

等比数列介绍：

等比数列是一种数列，其中相邻两项的比值是一个固定的常数，这个常数被称为公比。设等比数列的首项为a1，公比为q，则该数列的一般形式为：a1，a1×q，a1×q^2，a1×q^3等。

即首项为a1，后面的每一项都是前一项乘以公比q。这里的q可以是正的、负的或零，只要它不等于1，就可以构成一个等比数列。

等比数列有些特殊性质，从第二项开始，相邻两项之间的比值都是相等的，即a2/a1=a3/a2=a4/a3==q。从第n项开始，任意两项之间的比值都是相等的，即an/am=(an-1)/a(m-1)=q^(n-m)。

等比数列在数学中应用非常广泛，比如可以用于计算复利、等比年增长率、等比缩放等问题。此外，在物理、天文学、生态学等科学领域，等比数列也常常被用来描述各种自然现象的规律性。