几道极限的数学题……帮帮忙……

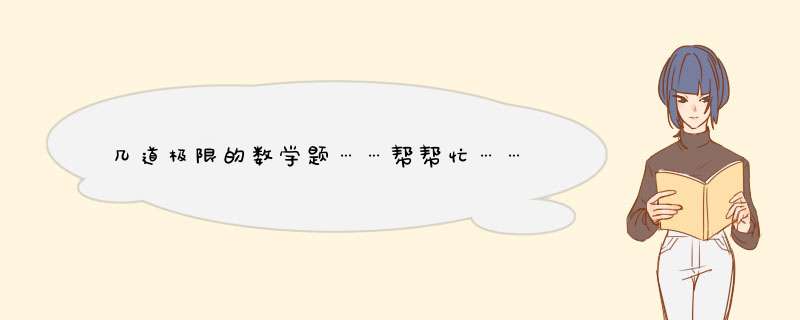
1。答案：-1 解： 因为lim(1/(1-x)-3/(1-x的三次方)) x→1 等于 lim(x^2+x-2)/(1-x的三次方） 当x=1时 (x^2+x-2)=0 （1-x的三次方）=0 所以用洛比达法则 lim(1/(1-x)-3/(1-x的三次方))=lim(x^2+x-2)/(1-x的三次方)=lim(2x+1)/(-3x^2) 当 x→1时 原式=（21+1)/(-31^2)= -1

2。答案：2^4/5^10 解： 因为分子n的最高次是n^6n^4=n^10 分母n的最高次是n^10 即相同 故 结果取最高次的系数比 2^4/5^10 3。 答案：∞ 解：因为当x→无穷时 2x三次方的增加趋势比x的增加趋势要大 故 ∞-∞=∞ ∞在+1=∞

1 分子与分母要都是趋近0极限才成立，1是(x平方+ax+b)一根，然后(x平方+ax+b=（x-1)(x+b)分解因式。。。

2 如果a不为o,a为常数那lim(a/x) 只能是无穷了，无穷没意义哪

3 limsin(nπ)n是整数sin(nπ)=0否则答案有问题了

不懂，晚上我在帮你解答

1 r=2a(1+cosθ), 极坐标的图像表示心型线，最早出现在笛卡尔写给他喜欢的人的一封情书上面！当然要对方也看得懂，就需要对方对数学有一定的了解！

2 [ -5e^(2iπ)+13]/2=14 这个方程式的主体部分来自于欧拉的著名公式（数学上最美的公式）：e^(2iπ)+1=0!!! 在这个公式里面依次出现了 5 2 i 1 3 1 4 意思可以理解为”我爱你一生一世“。 这个不需要数学基础。

3 （待补充）

如果n>m

分式上下两端都除于x^m

因为分子还有a(0)x^(n-m)等不为常数项，

所以极限不存在。

如果n=m

分式上下两端都除于x^m

分式上下都为常数

极限为a0/bb0

如果n<m

分式上下两端都除于x^n

分母还有不为常数项

极限为0