z=arccos(2-x^2+3y)的定义域？

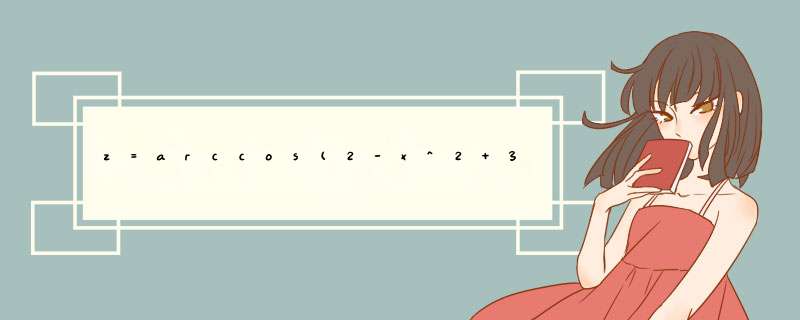
你好！根据三角函数arccos的定义，其定义域为[-1,1]。因此要求z=arccos(2-x^2+3y)的定义域，需要分别将 2-x^2+3y 和 -1, 1 进行比较大小，以确定z的取值范围。

首先可以通过解方程 2-x^2+3y = -1 或者 2-x^2+3y = 1 来确定z的边界值。我们有：

当 2-x^2+3y = -1 时，x^2+3y = 3，即 y = (3-x^2)/3，代入原式得到：

z = arccos(-2/3+x^2/3) 

由于cos函数的定义域为[-1,1]，所以-2/3+x^2/3的取值范围也是[-1,1]，即 x^2/3 <= 5/3。因此，x的取值范围为[-√15, √15]。

同理，当 2-x^2+3y = 1 时，代入原式得到：

z = arccos(4/3+x^2/3)

由于cos函数的定义域为[-1,1]，所以4/3+x^2/3的取值范围也是[-1,1]，即 x^2/3 <= -1/3。但由于平方根不可能是负数，所以没有实际意义。

综上所述，x的取值范围为[-√15, √15]，y的取值由于没有限制，可以是任意实数。因此z=arccos(2-x^2+3y)的定义域可以表示为：

(-√15, √15) × R

希望这个答案能够解决你的问题，如果还有疑问或者需要进一步解释，请随时追问。

（以上由“知否AI问答”回复，可以免费直接访问体验：网页链接）

1、首先第一步要打开计算器，摁第一排左侧的shift键；

2、紧接着摁“2”键，选择角度单位；

3、然后再摁“1”键；

4、再摁“shift”键。

5、这时候就能够摁第四排最右边的tan键，看到计算器显示屏上的tan有”-1“的角标。如下图所示；

6、最后就要输入4，再摁等号键，即可得到答案，如果想算arccos或者arcsin，只需把第五步中的tan换成sin或者cos，这样反函数就出来了，如下图所示。

以下为非基本数学函数的列表，皆可由基本数学函数导出：

函数

由基本函数导出之公式

Secant（正割）

Sec(X)

=

1

/

Cos(X)

Cosecant（余割）

Cosec(X)

=

1

/

Sin(X)

Cotangent（余切）

Cotan(X)

=

1

/

Tan(X)

Inverse

Sine

（反正弦）

Arcsin(X)

=

Atn(X

/

Sqr(-X

X

+

1))

Inverse

Cosine

（反余弦）

Arccos(X)

=

Atn(-X

/

Sqr(-X

X

+

1))

+

2

Atn(1)

Inverse

Secant

（反正割）

Arcsec(X)

=

Atn(X

/

Sqr(X

X

-

1))

+

Sgn((X)

-

1)

(2

Atn(1))

Inverse

Cosecant

（反余割）

Arccosec(X)

=

Atn(X

/

Sqr(X

X

-

1))

+

(Sgn(X)

-

1)

(2

Atn(1))

Inverse

Cotangent

（反余切）

Arccotan(X)

=

Atn(X)

+

2

Atn(1)

Hyperbolic

Sine

（双曲正弦）

HSin(X)

=

(Exp(X)

-

Exp(-X))

/

2

Hyperbolic

Cosine

（双曲余弦）

HCos(X)

=

(Exp(X)

+

Exp(-X))

/

2

Hyperbolic

Tangent

（双曲正切）

HTan(X)

=

(Exp(X)

-

Exp(-X))

/

(Exp(X)

+

Exp(-X))

Hyperbolic

Secant

（双曲正割）

HSec(X)

=

2

/

(Exp(X)

+

Exp(-X))

Hyperbolic

Cosecant（双曲余割）

HCosec(X)

=

2

/

(Exp(X)

-

Exp(-X))

Hyperbolic

Cotangent（双曲余切）

HCotan(X)

=

(Exp(X)

+

Exp(-X))

/

(Exp(X)

-

Exp(-X))

Inverse

Hyperbolic

Sine（反双曲正弦）

HArcsin(X)

=

Log(X

+

Sqr(X

X

+

1))

Inverse

Hyperbolic

Cosine（反双曲余弦）

HArccos(X)

=

Log(X

+

Sqr(X

X

-

1))

Inverse

Hyperbolic

Tangent（反双曲正切）

HArctan(X)

=

Log((1

+

X)

/

(1

-

X))

/

2

Inverse

Hyperbolic

Secant（反双曲正割）

HArcsec(X)

=

Log((Sqr(-X

X

+

1)

+

1)

/

X)

Inverse

Hyperbolic

Cosecant

HArccosec(X)

=

Log((Sgn(X)

Sqr(X

X

+

1)

+

1)

/

X)

Inverse

Hyperbolic

Cotangent

（反双曲余切）

HArccotan(X)

=

Log((X

+

1)

/

(X

-

1))

/

2

以N

为底的对数

LogN(X)

=

Log(X)

/

Log(N)

sinA＝对边/斜边，cosA＝邻边/斜边；sin60度＝1/2，sin45度＝根号2/2；cos60度＝根号3/2，cosπ/4＝根号2/2。

三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具。在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许它们的取值扩展到任意实数值，甚至是复数值。

在直角三角形中，当平面上的三点A、B、C的连线，AB、AC、BC，构成一个直角三角形，其中∠ACB为直角。对∠BAC而言，对边（opposite）a=BC、斜边（hypotenuse）c=AB、邻边（adjacent）b=AC。

扩展资料：

级数定义

只使用几何和极限的性质，可以证明正弦的导数是余弦，余弦的导数是负的正弦。（在微积分中，所有角度都以弧度来度量）。我们可以接着使用泰勒级数的理论来证明下列恒等式对于所有实数x都成立：

这些恒等式经常被用做正弦和余弦函数的定义。它们经常被用做三角函数的严格处理和应用的起点（比如，在傅里叶级数中），因为无穷级数的理论可从实数系的基础上发展而来，不需要任何几何方面的考虑。这样，这些函数的可微性和连续性便可以单独从级数定义来确立。

其他级数可见于：

注：Un是n次上/下数， Bn是n次伯努利数，∣x∣<π/2。

参考资料：

是反三角函数

反三角函数实际上并不能叫做函数，因为它并不满足一个自变量对应一个函数值的要求，其图像与其原函数关于函数y=x对称。其概念首先由欧拉提出，并且首先使用了arc+函数名的形式表示反三角函数，而不是f-1(x)

　　反三角函数主要是三个：

　　y=arcsin(x)，定义域[-1,1]，值域[-π/2,π/2]，图象用红色线条；

　　y=arccos(x)，定义域[-1,1]，值域[0,π]，图象用蓝色线条；

　　y=arctan(x)，定义域(-∞，+∞)，值域(-π/2,π/2)，图象用绿色线条；

　　sinarcsin(x)=x,定义域[-1,1],值域 -π/2,π/2

　　证明方法如下：设arcsin(x)=y,则sin(y)=x ,将这两个式子代入上式即可得