sin3Xtan5X，X→派，用洛必达法则求下列极限

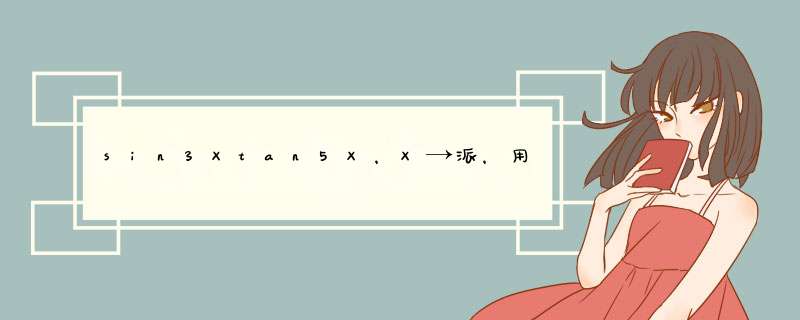
limsin3X/tan5X=-3/5（X→π）。

解：

方法1

limsin3X/tan5X=limsin3xcos5x/sin5x

=lim(1/2)(sin8x-sin2x)/sin5x（积化和差）

=lim(1/2)(8cos8x-2cos2x)/5cos5x（分子分母同时求导）

=（1/2）(8-2)/(-5)

=-3/5

方法2

limsin3x/tan5x

=limcos3x 3 / sec^2 5x 5(分子分母同时求导)

=3/5lim cos3x (cos5x)^2

=3/5 (-1)(-1)^2

=-3/5

扩展资料：

极限的求法有很多种：

1、连续初等函数，在定义域范围内求极限，可以将该点直接代入得极限值，因为连续函数的极限值就等于在该点的函数值。

2、利用恒等变形消去零因子（针对于0/0型）。

3、利用无穷大与无穷小的关系求极限。

4、利用无穷小的性质求极限。

5、利用等价无穷小替换求极限，可以将原式化简计算。

6、利用两个极限存在准则，求极限，有的题目也可以考虑用放大缩小，再用夹逼定理的方法求极限。

7、利用两个重要极限公式求极限。

方法一：

可以转化成lim，

X趋向0（sin3x／sin5x）＊cos5x＝lim，

X趋向0（3x／5x）＊cos5x＝3／5＊cos5x

而当lim，X趋向0cos5x＝1

所以就知道原式＝3／5。

方法二：

解：

这里的sin3x和tan5x，不能直接换成3x，和5x，

因为x→π时，x本身不是无穷小。

你可以令x－π＝t。

则x＝t＋π，这样x→π时，t→0

有limsin3x／tan5x

＝sin3（t＋π）／tan5（t＋π）

＝－sin3t／tan5t

＝－3／5

方法三：

这里的sin3x和tan5x，不能直接换成3x，和5x，因为x→π时，x本身不是无穷小．

可以令x－π＝t，则x＝t＋π，这样x→π时，t→0

有limsin3x／tan5x＝sin3（t＋π）／tan5（t＋π）

＝－sin3t／tan5t＝－3／5

方法四：

令t=x-π,则t->0

原式=limx->π sin3x/tan5x

=limt->0 sin3(t+π)/tan5(t+π)

=limt->0 -sin3t/tan5t

=limt->0 -3t/5t

=-3/5

以下是洛必达法则：

=limx->π sin3x/tan5x若直接代入x=π,原式呈0/0型，故可用洛必达法则。

=limx->π 3cos3x/5(sec5x)^2

=limx->π 3cos3x(cos5x)^2/5

=3(-1)(-1)^2/5=-3/5 

补充：就是代进去，cos3π=cosπ=-1。

扩展资料

举例：

sin3x～3xtan5x～5x

条件是x→0

而本题条件是x→π

sinx＝－sin3（x－π）

tan5x＝tan5（x－π）

此时sin3（x－π）～3（x－π）tan5（x－π）～（x－π

lim（x→π）sin3x／tan5x

＝lim（x→π）－sin3（x－π）／tan5（x－π）

＝lim（x→π）－3（x－π）／5（x－π）

＝－3／5

首先你的第一题的答案是错的，应该是a/b。

(5)

lim(1-x)tan(πx/2)

=lim(1-x)sin(πx/2)/cos(πx/2)

=lim[(1-x)cos(π/2-πx/2)/sin(π/2-πx/2)]

=limcos[π/2(1-x)]/{limsin[π/2(1-x)]/(1-x)}

=1/(π/2)

=2/π

(6)

lim(1+sinx-cosx)/(1+sinpx-cospx)

=lim[2sinx/2cosx/2+2(sinx/2)^2]/[2sinpx/2cospx/2+2(sinpx/2)^2]

=lim[sinx/2(cosx/2+sinx/2)]/[sinpx/2(cospx/2+sinpx/2)]

=lim[sinx/2sin(x/2+π/4)]/[sinpx/2sin(px/2+π/4)]

(上下同除px/2）

=1/plim[sinx/2/(x/2)]limsin(x/2+π/4)/{lim[sinpx/2/(px/2)]limsin(px/2+π/4)}

=1/p1sinπ/4/{1sinπ/4}

=1/p

使用和差化积是对的,但是楼上的后面写错了……

原式=lim{2sin[(√(x+1)-√x)]/2cos[√(x+1)+√x]/2}

x→+∞

因为cos[√(x+1)+√x]/2}有范围,属于[-1,1]；

而limsin[(√(x+1)-√x)]/2]=o

x→+∞

所以原式=0

原式=lim(x趋于1)lim(y趋于1)sin(x-y)/(x²-y²)

=lim(x趋于1)sin(x-1)/(x²-1)

=lim(x趋于1)sin(x-1)/[(x-1)(x+1)]

sin(x-1)和x-1为等价无穷小，所以极限为1/2

或对lim(x趋于1)sin(x-1)/(x²-1)用洛必达法则，得

lim(x趋于1)cos(x-1)/(2x)=1/2