从3名男生和2名女生中任选2人参加演讲比赛

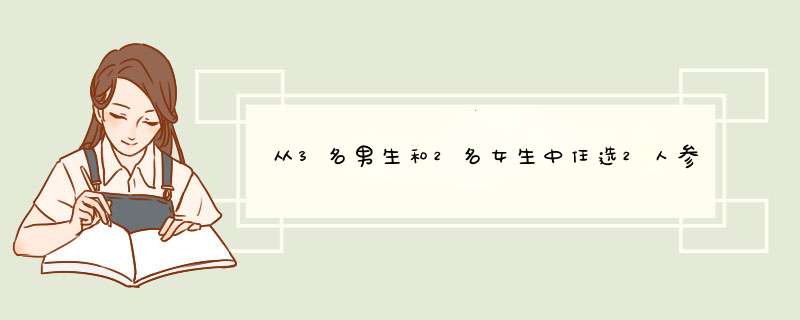
1、先从5人中任取一人是男生的概率为3/5。再从剩下的4人中选一个男生的概率为2/4，所以都是男生的概率为3/52/4=3/10

2、若先抽中男生再抽中女生，概率为3/52/4=3/10；若先抽中女生再抽中男生，概率为2/53/4=3/10。所以最终答案为3/10+3/10=3/5

3、先选中甲的概率为1/5。 后选中甲的概率为4/51/4=1/5。最后答案为1/5+1/5=2/5

解1：正面做比较麻烦，考虑反面做，没有女生的概率是（C43/C63）至少有一个女生概率就是

P=1-(C43/c63)=08

第二题你能不能先把括号加上去啊。。。。（虽然不一定会做~）

至少一名女生，即1个或2个或3个，

0个，概率为4C3 / 7C3 = 4/35, (4C3是指4个中选3个的组合数，4C3=4, 7C3=35，下同)

剩下的就是至少一名女生的概率，即1-4/35=31/35。

P[X=k] = 4Ck 3C(3-k) / 7C3，期望为12/7名

首先，对立事件肯定是互斥事件。

1、互斥。因为不可能同时恰好有一个又有两个男生，但是还有0个男生的情况，所以仅互斥，不对立、

2、都不是，因为一个男生和一个女生恰好满足，不互斥，当然也不对立。

3、都不是，至少有一名男生包含了全是男生的情况。

4、互斥，对立。全是女生即0个男生的情况，至少一个男生即1个和两个男生的情况，所以互斥又对立。