（2014?浦东新区二模）已知：如图，在正方形ABCD中，点E是边AD的中点，联结BE，过点A作AF⊥BE，分别交BE

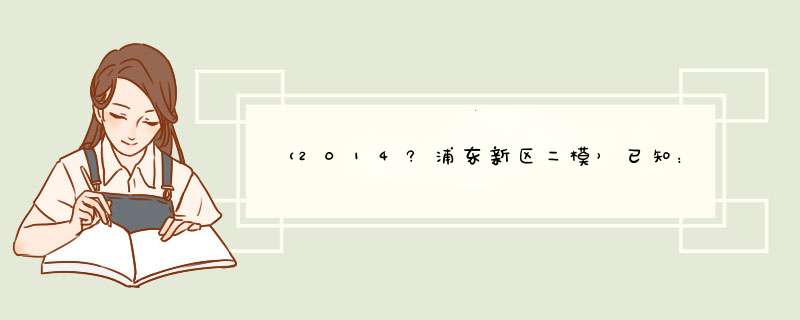
解答：证明：（1）∵四边形ABCD是正方形，
∴AB=DA=BC=CD，∠BAD=∠ADF=∠BCF=90°，
∴∠BAH+∠HAE=90°，
∵AF⊥BE，
∴∠AHB=90°，
即∠BAH+∠ABH=90°，
∴∠ABH=∠HAE，
又∵∠BAE=∠ADF，
∴△ABE∽△DAF，
∴

AB

DA

=

AE

DF

，
∴AE=DF，
∵点E是边AD的中点，
∴点F是边DC的中点，
∴CF=AE，
在Rt△ABE与Rt△CBF中，

AB＝CD AE＝CF

∴Rt△ABE≌Rt△CBF（HL），
∴BE=BF．

（2）∵四边形ABCD是正方形，
∴DB平分∠ADC，
∴∠ADB=∠CDB，
在△DEO与△DFO中，

ED＝FD ∠ADB＝∠CDB DO＝DO

∴△DEO≌△DFO（SAS），
∴∠DEO=∠DFO，
∵△ABE∽△DAF，
∴∠AEB=∠DFA，
∴∠AEB=∠DEO．